Page 73 - Contributed Paper Session (CPS) - Volume 8

CPS2187 Lukasz Widla-Domaradzki
4) Because estimates for the model A3 are known, I can now merge
analytically both models. In this case my anchor will show strength of
the connection between model A2 and A3.

3. Result
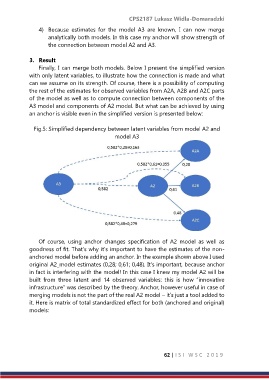
Finally, I can merge both models. Below I present the simplified version
with only latent variables, to illustrate how the connection is made and what
can we assume on its strength. Of course, there is a possibility of computing
the rest of the estimates for observed variables from A2A, A2B and A2C parts
of the model as well as to compute connection between components of the
A3 model and components of A2 model. But what can be achieved by using
an anchor is visible even in the simplified version is presented below:

Fig.5: Simplified dependency between latent variables from model A2 and
model A3

Of course, using anchor changes specification of A2 model as well as
goodness of fit. That’s why it’s important to have the estimates of the non-
anchored model before adding an anchor. In the example shown above I used
original A2_model estimates (0,28; 0,61; 0,48). It’s important, because anchor
in fact is interfering with the model! In this case I knew my model A2 will be
built from three latent and 14 observed variables: this is how “innovative
infrastructure” was described by the theory. Anchor, however useful in case of
merging models is not the part of the real A2 model – it’s just a tool added to
it. Here is matrix of total standardized effect for both (anchored and original)
models:

62 | I S I W S C 2 0 1 9