Page 45 - Contributed Paper Session (CPS) - Volume 6

CPS1484 Neela A Gulanikar et al.
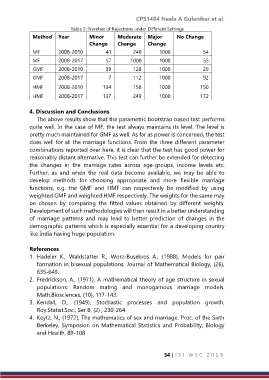
Table 2: Number of Rejections under Different Settings
Method Year Minor Moderate Major No Change
Change Change Change
MF 2008-2010 41 240 1000 54
MF 2008-2017 57 1000 1000 55
GMF 2008-2010 39 128 1000 29
GMF 2008-2017 7 112 1000 92
HMF 2008-2010 134 158 1000 150
HMF 2008-2017 137 249 1000 172

4. Discussion and Conclusions
The above results show that the parametric bootstrap based test performs
quite well. In the case of MF, the test always maintains its level. The level is
pretty much maintained for GMF as well. As far as power is concerned, the test
does well for all the marriage functions. From the three different parameter
combinations reported over here, it is clear that the test has good power for
reasonably distant alternative. This test can further be extended for detecting
the changes in the marriage rates across age-groups, income levels etc.
Further, as and when the real data become available, we may be able to
develop methods for choosing appropriate and more flexible marriage
functions, e.g. the GMF and HMF can respectively be modified by using
weighted GMF and weighted HMF respectively. The weights for the same may
be chosen by comparing the fitted values obtained by different weights.
Development of such methodologies will then result in a better understanding
of marriage patterns and may lead to better prediction of changes in the
demographic patterns which is especially essential for a developing country
like India having huge population.

References
1. Hadeler K., Waldstatter R., Worz-Busekros A., (1988), Models for pair
formation in bisexual populations, Journal of Mathematical Biology, (26),
635-649.
2. Fredrickson, A., (1971), A mathematical theory of age structure in sexual
populations: Random mating and monogamous marriage models.
Math.Biosciences, (10), 117-143.
3. Kendall, D., (1949), Stochastic processes and population growth.
Roy.Statist.Soc., Ser B, (2) , 230-264.
4. Keytz, N., (1972), The mathematics of sex and marriage. Proc. of the Sixth
Berkeley, Symposion on Mathematical Statistics and Probability, Biology
and Health, 89-108

34 | I S I W S C 2 0 1 9