Page 51 - Special Topic Session (STS) - Volume 3

STS515 Alison L. G. et al.
in the future (Zheng, 2017). New fields of application are constantly emerging,
dealing with increasingly complex data such as high-dimensional sequence or
network data, and generating new types of problems that statisticians are
called to address. This shifting landscape makes it difficult for statistics
educators to foresee students’ needs, let alone cater to them through
curricular reform, a typically slow and gradual process. Instead of trying to
anticipate every development, we believe our programs should prepare
students to be able to adapt to these changes on their own. We borrow the
term “adaptive expertise” from the fields of cognitive development and
pedagogy to refer to such desired behaviour.
The concept of adaptive expertise was introduced by Hatano & Inagaki
(1986) to describe the ability to aptly address new types of problems, as
opposed to routine expertise which is focused on efficiently solving familiar
problems. It is closely related to the concept of transfer of learning, i.e. “the
ability to extend what has been learned in one context to new contexts” (NRC,
2000), but we prefer the term adaptive expertise as it encompasses both
knowledge and practice. We first look at a general framework for attaining
adaptive expertise, one that also offers an interesting lens on Statistics
Education, before going on to propose specific strategies.

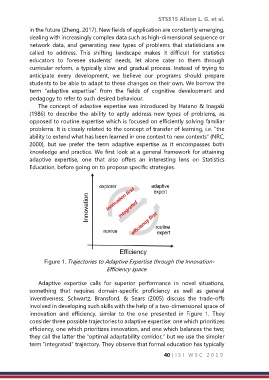
Figure 1. Trajectories to Adaptive Expertise through the Innovation-
Efficiency space.

Adaptive expertise calls for superior performance in novel situations,
something that requires domain-specific proficiency as well as general
inventiveness. Schwartz, Bransford, & Sears (2005) discuss the trade-offs
involved in developing such skills with the help of a two-dimensional space of
innovation and efficiency, similar to the one presented in Figure 1. They
consider three possible trajectories to adaptive expertise: one which prioritizes
efficiency, one which prioritizes innovation, and one which balances the two;
they call the latter the “optimal adaptability corridor,” but we use the simpler
term “integrated” trajectory. They observe that formal education has typically
40 | I S I W S C 2 0 1 9