Page 31 - Contributed Paper Session (CPS) - Volume 3

CPS1934 Atikur R. K. et al.
weather station, we compute rolling mean ℎ (|) and rolling standard
̅

deviation (|) of relative humidity. In the next section, we explore underlying
ℎ
characteristics of (|) and (|) for = 1, … , and = 1, … , on
ℎ
RTI episodes where is the length of the time series considered for the th

weather station and is the number of weather stations.

3. Result
We use heatmap to explore the impact of rolling standard deviations of
temperature difference and relative humidity on RTI episodes. Results shown
in Figure 1 are test statistics computed for the null hypothesis : =
0

where is the proportion of days in the dataset with positive counts for RTI
0
episodes across all weather stations. Figure 1 clearly shows a region with
rolling standard deviation of relative humidity greater than or equal to 6 with
an indication that for this level of rolling standard deviation of relative
humidity is likely to increase the RTI episodes.

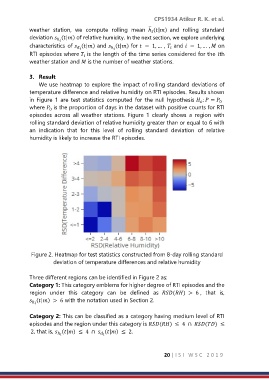
Figure 2. Heatmap for test statistics constructed from 8-day rolling standard
deviation of temperature differences and relative humidity

Three different regions can be identified in Figure 2 as:
Category 1: This category emblems for higher degree of RTI episodes and the
region under this category can be defined as () > 6 , that is,
(|) > 6 with the notation used in Section 2.
ℎ

Category 2: This can be classified as a category having medium level of RTI
episodes and the region under this category is () ≤ 4 ∩ () ≤
2, that is, (|) ≤ 4 ∩ (|) ≤ 2.
ℎ

20 | I S I W S C 2 0 1 9