Page 52 - Contributed Paper Session (CPS) - Volume 3

CPS1943 Nandish C. et al.
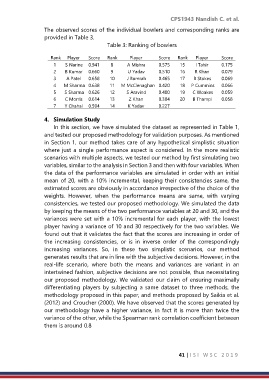
The observed scores of the individual bowlers and corresponding ranks are
provided in Table 3.
Table 3: Ranking of bowlers

Rank Player Score Rank Player Score Rank Player Score
1 S Narine 0.941 8 A Mishra 0.575 15 I Tahir 0.175
2 B Kumar 0.660 9 U Yadav 0.510 16 R Khan 0.079
3 A Patel 0.658 10 J Bumrah 0.465 17 B Stokes 0.069
4 M Sharma 0.638 11 M McClenaghan 0.420 18 P Cummins 0.066
5 S Sharma 0.626 12 S Aravind 0.400 19 C Woakes 0.059
6 C Morris 0.614 13 Z Khan 0.304 20 B Thampi 0.058
7 Y Chahal 0.594 14 K Yadav 0.227

4. Simulation Study
In this section, we have simulated the dataset as represented in Table 1,
and tested our proposed methodology for validation purposes. As mentioned
in Section 1, our method takes care of any hypothetical simplistic situation
where just a single performance aspect is considered. In the more realistic
scenarios with multiple aspects, we tested our method by first simulating two
variables, similar to the analysis in Section 3 and then with four variables. When
the data of the performance variables are simulated in order with an initial
mean of 20, with a 10% incremental, keeping their consistencies same, the
estimated scores are obviously in accordance irrespective of the choice of the
weights. However, when the performance means are same, with varying
consistencies, we tested our proposed methodology. We simulated the data
by keeping the means of the two performance variables at 20 and 30, and the
variances were set with a 10% incremental for each player, with the lowest
player having a variance of 10 and 30 respectively for the two variables. We
found out that it validates the fact that the scores are increasing in order of
the increasing consistencies, or is in inverse order of the correspondingly
increasing variances. So, in these two simplistic scenarios, our method
generates results that are in line with the subjective decisions. However, in the
real-life scenario, where both the means and variances are variant in an
intertwined fashion, subjective decisions are not possible, thus necessitating
our proposed methodology. We validated our claim of ensuring maximally
differentiating players by subjecting a same dataset to three methods, the
methodology proposed in this paper, and methods proposed by Saikia et al.
(2012) and Croucher (2000). We have observed that the scores generated by
our methodology have a higher variance, in fact it is more than twice the
variance of the other, while the Spearman rank correlation coefficient between
them is around 0.8

41 | I S I W S C 2 0 1 9