Page 54 - Contributed Paper Session (CPS) - Volume 3

CPS1943 Nandish C. et al.
10 0.9 0.4 0.7 0.5 0.5 0.4 0.6
0.9 15 0.8 0.5 0.6 0.8 0.4 0.3
0.4 0.8 20 0.6 0.9 0.3 0.4 0.9

∑ = 0.7 0.5 0.6 21 0.3 0.4 0.8 0.9
0.5 0.6 0.9 0.3 17 0.4 0.3 0.8
0.5 0.8 0.3 0.4 0,4 23 0.4 0.9
0.4 0.4 0.4 0.8 0,3 0.4 14 0.9
[0,6 0.3 0.9 0.9 0.8 0.9 0.9 22]

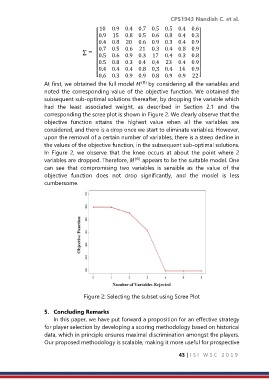
At first, we obtained the full model (8) by considering all the variables and
noted the corresponding value of the objective function. We obtained the
subsequent sub-optimal solutions thereafter, by dropping the variable which
had the least associated weight, as described in Section 2.1 and the
corresponding the scree plot is shown in Figure 2. We clearly observe that the
objective function attains the highest value when all the variables are
considered, and there is a drop once we start to eliminate variables. However,
upon the removal of a certain number of variables, there is a steep decline in
the values of the objective function, in the subsequent sub-optimal solutions.
In Figure 2, we observe that the knee occurs at about the point where 2
variables are dropped. Therefore, (6) appears to be the suitable model. One
can see that compromising two variables is sensible as the value of the
objective function does not drop significantly, and the model is less
cumbersome.

Figure 2: Selecting the subset using Scree Plot

5. Concluding Remarks
In this paper, we have put forward a proposition for an effective strategy
for player selection by developing a scoring methodology based on historical
data, which in principle ensures maximal discrimination amongst the players.
Our proposed methodology is scalable, making it more useful for prospective

43 | I S I W S C 2 0 1 9