Page 31 - Contributed Paper Session (CPS) - Volume 4

CPS2107 Junfan Tao et al.
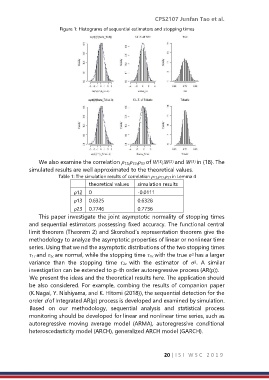
Figure 1: Histograms of sequential estimators and stopping times

We also examine the correlation ρ12,ρ23,ρ13 of W ,W and W in (18). The
(3)
(1)
(2)
simulated results are well approximated to the theoretical values.
Table 1: The simulation results of correlation ρ12,ρ13,ρ23 in Lemma 4
theoretical values simulation results
ρ12 0 -0.0111
ρ13 0.6325 0.6328
ρ23 0.7746 0.7736
This paper investigate the joint asymptotic normality of stopping times
and sequential estimators possessing fixed accuracy. The functional central
limit theorem (Theorem 2) and Skorohod’s representation theorem give the
methodology to analyze the asymptotic properties of linear or nonlinear time
series. Using that we nd the asymptotic distributions of the two stopping times

τ1c and τ2c are normal, while the stopping time τ1c with the true σ has a larger
2
variance than the stopping time τ2c with the estimator of σ . A similar
2
investigation can be extended to p-th order autoregressive process (AR(p)).
We present the ideas and the theoretical results here. The application should
be also considered. For example, combing the results of companion paper
(K.Nagai, Y. Nishiyama, and K. Hitomi (2018)), the sequential detection for the
order d of Integrated AR(p) process is developed and examined by simulation.
Based on our methodology, sequential analysis and statistical process
monitoring should be developed for linear and nonlinear time series, such as
autoregressive moving average model (ARMA), autoregressive conditional
heteroscedasticity model (ARCH), generalized ARCH model (GARCH).

20 | I S I W S C 2 0 1 9