Page 160 - Contributed Paper Session (CPS) - Volume 2

CPS1488 Willem van den B. et al.
Let µIS and ΣIS denote the importance sampling estimates of the mean and
1 2
covariance, respectively, of () {− 2 2 || − ()|| }. Then, the EP
\

updates of matching the moments in (4) follow as
= ∑ −1 IS − and Λ = ∑ −1 −Λ . (7)

\
IS

\
IS
Here, ΣIS is a sample covariance matrix and it is challenging to estimate its
( + 1)/2 elements from importance samples. We therefore regularize ΣIS
and consider two options for this. With linearization, we had Λ = Λ in (6)

such that nk is an upper limit to its rank. One regularization is therefore to
adjust ΣIS in (7) such that only a limited number of largest eigenvalues of Λk are
nonzero. This regularization will hurt approximation accuracy less if the map
HSk is smoother. Another regularization can come from the problem context in
(1). For instance in the heat equation example, where f is the temperature
distribution, both the prior and posterior covariance of f could be expected to
concentrate near the diagonal since temperatures close to each other influence
each other more than those further apart. We can exploit this by covariance
tapering (Furrer et al., 2006) of ΣIS as a form of regularization. We use the
Wendland1 taper as given in Furrer et al. (2006, Table 1). Algorithm 1
summarizes EP-IS.

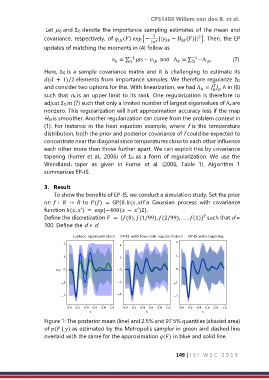
3. Result
To show the benefits of EP-IS, we conduct a simulation study. Set the prior
on ∶ → to () = GP{0, (, 0′a Gaussian process with covariance
function (, ′) = exp{−400( − ′)2}.
Define the discretization = {(0), (1/99), (2/99), . . . , (1)} such that d =

100. Define the d × d

f(x)

Figure 1: The posterior mean (line) and 2.5% and 97.5% quantiles (shaded area)
of ( | ) as estimated by the Metropolis sampler in green and dashed line
overlaid with the same for the approximation () in blue and solid line.

149 | I S I W S C 2 0 1 9