Page 224 - Contributed Paper Session (CPS) - Volume 2

CPS1834 Gumgum D. et al.
4. Result
<The result of fit SARIMA modeling based on two calendars can be seen below.

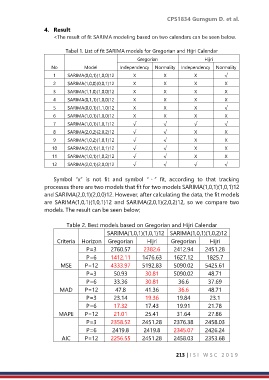
Tabel 1. List of fit SARIMA models for Gregorian and Hijri Calendar
Gregorian Hijri
No Model Independency Normality Independency Normality
1 SARIMA(0,0,1)(1,0,0)12 X X X √
2 SARIMA(1,0,0)(0,0,1)12 X X X X
3 SARIMA(1,1,0)(1,0,0)12 X X X X
4 SARIMA(0,1,1)(1,0,0)12 X X X X
5 SARIMA(0,0,1)(1,1,0)12 X X X √
6 SARIMA(1,0,1)(1,0,0)12 X X X X
7 SARIMA(1,0,1)(1,0,1)12 √ √ √ √
8 SARIMA(2,0,2)(2,0,2)12 √ √ X X
9 SARIMA(1,0,2)(1,0,1)12 √ √ X X
10 SARIMA(2,0,1)(1,0,1)12 √ √ X X
11 SARIMA(1,0,1)(1,0,2)12 √ √ X X
12 SARIMA(2,0,1)(2,0,0)12 √ √ √ √

Symbol “x” is not fit and symbol “ ” fit, according to that tracking
processes there are two models that fit for two models SARIMA(1,0,1)(1,0,1)12
and SARIMA(2,0,1)(2,0,0)12. However, after calculating the data, the fit models
are SARIMA(1,0,1)(1,0,1)12 and SARIMA(2,0,1)(2,0,2)12, so we compare two
models. The result can be seen below;

Table 2. Best models based on Gregorian and Hijri Calendar
SARIMA(1,0,1)(1,0,1)12 SARIMA(1,0,1)(1,0,2)12
Criteria Horizon Gregorian Hijri Gregorian Hijri
P=3 2760.57 2382.6 2412.94 2451.28
P=6 1412.11 1476.63 1627.12 1825.7
MSE P=12 4333.97 5192.83 5090.02 5425.61
P=3 50.93 30.81 5090.02 48.71
P=6 33.36 30.81 36.6 37.69
MAD P=12 47.8 41.36 36.6 48.71
P=3 23.14 19.36 19.84 23.1
P=6 17.32 17.43 19.91 21.78
MAPE P=12 21.01 25.41 31.64 27.86
P=3 2358.52 2451.28 2376.38 2458.03
P=6 2419.8 2419.8 2345.07 2426.24
AIC P=12 2256.55 2451.28 2458.03 2353.68

213 | I S I W S C 2 0 1 9