Page 17 - Contributed Paper Session (CPS) - Volume 4

CPS2101 Bertail Patrice et al.
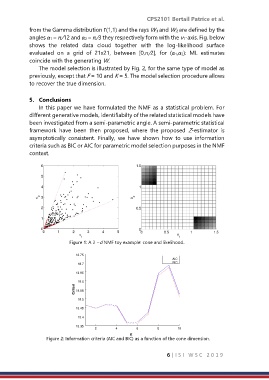
from the Gamma distribution Γ(1,1) and the rays W.1 and W.2 are defined by the
angles α1 = π/12 and α2 = π/3 they respectively form with the v1-axis. Fig. below
shows the related data cloud together with the log-likelihood surface
evaluated on a grid of 21x21, between [0,π/2], for (α1,α2): ML estimates
coincide with the generating W.
The model selection is illustrated by Fig. 2, for the same type of model as
previously, except that F = 10 and K = 5. The model selection procedure allows
to recover the true dimension.

5. Conclusions
In this paper we have formulated the NMF as a statistical problem. For
different generative models, identifiabilty of the related statistical models have
been investigated from a semi-parametric angle. A semi-parametric statistical
framework have been then proposed, where the proposed Z-estimator is
asymptotically consistent. Finally, we have shown how to use information
criteria such as BIC or AIC for parametric model selection purposes in the NMF
context.

Figure 1: A 2 −d NMF toy example: cone and likelihood.

18.75
AIC
18.7 BIC

18.65
18.6
18.55
18.5
18.45
18.4
18.35
2 4 6 8 10
K
Figure 2: Information criteria (AIC and BIC) as a function of the cone dimension.

6 | I S I W S C 2 0 1 9