Page 32 - Contributed Paper Session (CPS) - Volume 5

CPS657 Folorunso Serifat A. et al.
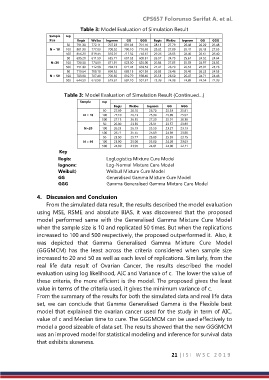
Table 3: Model Evaluation of Simulation Result
Sample rep
Size llogis Weibu lognom GG GGG llogis Weibu lognom GG GGG
50 791.30 772.11 707.23 691.03 701.10 28.13 27.79 26.48 26.29 26.48
N = 10 100 801.90 777.03 700.52 700.10 710.40 28.32 27.89 26.47 26.45 27.65
500 856.20 819.45 810.01 711.32 750.61 29.26 28.63 28.46 26.67 26.40
50 695.20 611.59 655.71 601.33 609.31 26.37 24.73 25.61 24.52 24.64
N=20 100 720.50 774.63 671.91 623.50 620.90 26.84 27.83 25.92 24.97 24.92
500 751.30 712.98 704.13 671.45 663.53 27.41 26.70 26.53 25.91 25.76
50 719.64 700.18 699.52 689.15 601.59 26.83 26.46 26.45 26.25 24.53
N = 50 100 703.90 707.48 700.85 610.79 598.40 26.53 26.60 26.47 24.71 24.46
500 644.59 623.90 619.61 602.10 501.37 25.39 24.98 24.89 24.54 22.39

Table 3: Model Evaluation of Simulation Result (Continued…)
Sample rep
Size llogis Weibu lognom GG GGG
50 27.89 26.10 26.70 25.33 25.81
N = 10 100 27.10 26.23 25.90 25.89 25.97
500 27.15 26.55 27.20 25.91 26.38
50 26.00 23.59 25.31 23.57 23.89
N=20 100 26.23 26.19 25.50 23.27 23.13
500 26.71 25.55 25.89 24.89 23.80
50 25.50 25.77 25.83 25.59 23.15
N = 50 100 25.90 25.98 25.80 24.08 23.03
500 24.89 23.95 24.01 24.00 22.11
Key
llogis: LogLogistics Mixture Cure Model
lognom: Log-Normal Mixture Cure Model
Weibul:} Weibull Mixture Cure Model
GG Generalised Gamma Mixture Cure Model
GGG Gamma Generalised Gamma Mixture Cure Model

4. Discussion and Conclusion
From the simulated data result, the results described the model evaluation
using MSE, RSME and absolute BIAS, it was discovered that the proposed
model performed same with the Generalised Gamma Mixture Cure Model
when the sample size is 10 and replicated 50 times. But when the replications
increased to 100 and 500 respectively, the proposed outperformed it. Also, it
was depicted that Gamma Generalised Gamma Mixture Cure Model
(GGGMCM) has the least across the criteria considered when sample size
increased to 20 and 50 as well as each level of replications. Similarly, from the
real life data result of Ovarian Cancer, the results described the model
evaluation using log likelihood, AIC and Variance of c. The lower the value of
these criteria, the more efficient is the model. The proposed gives the least
value in terms of the criteria used, it gives the minimum variance of c.
From the summary of the results for both the simulated data and real life data
set, we can conclude that Gamma Generalised Gamma is the Flexible best
model that explained the ovarian cancer used for the study in term of AIC,
value of c and Median time to cure. The GGGMCM can be used effectively to
model a good sizeable of data set. The results showed that the new GGGMCM
was an improved model for statistical modeling and inference for survival data
that exhibits skewness.

21 | I S I W S C 2 0 1 9