Page 15 - Contributed Paper Session (CPS) - Volume 8

CPS2144 Laura Antonucci et al.
3. Result
We performed 10,000 permutation tests using the Fisher omnibus
combining function, considering different situations: the whole set of
implants, the upper and lower arch and front and back mouth.
The whole set of implants
In the first instance we considered the whole set of implants regardless
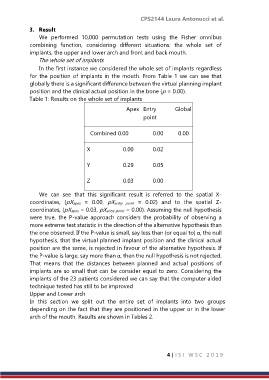
for the position of implants in the mouth. From Table 1 we can see that
globally there is a significant difference between the virtual planning implant
position and the clinical actual position in the bone (p = 0.00).
Table 1: Results on the whole set of implants
Apex Entry Global
point

Combined 0.00 0.00 0.00

X 0.00 0.02

Y 0.29 0.05

Z 0.03 0.00

We can see that this significant result is referred to the spatial X-
coordinates, (pXapex = 0.00, pXentry point = 0.02) and to the spatial Z-
coordinates, (pXapex = 0.03, pXentry point = 0.00). Assuming the null hypothesis
were true, the P-value approach considers the probability of observing a
more extreme test statistic in the direction of the alternative hypothesis than
the one observed. If the P-value is small, say less than (or equal to) α, the null
hypothesis, that the virtual planned implant position and the clinical actual
position are the same, is rejected in favour of the alternative hypothesis. If
the P-value is large, say more than α, then the null hypothesis is not rejected.
That means that the distances between planned and actual positions of
implants are so small that can be consider equal to zero. Considering the
implants of the 23 patients considered we can say that the computer aided
technique tested has still to be improved
Upper and Lower arch
In this section we split out the entire set of implants into two groups
depending on the fact that they are positioned in the upper or in the lower
arch of the mouth. Results are shown in Tables 2.

4 | I S I W S C 2 0 1 9