Page 23 - Contributed Paper Session (CPS) - Volume 8

CPS2151 Sarah B. Balagbis
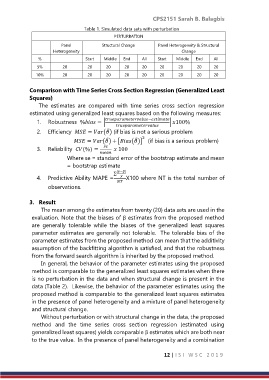
Table 1. Simulated data sets with perturbation
PERTURBATION
Panel Structural Change Panel Heterogeneity & Structural
Heterogeneity Change
% Start Middle End All Start Middle End All
5% 20 20 20 20 20 20 20 20 20
10% 20 20 20 20 20 20 20 20 20

Comparison with Time Series Cross Section Regression (Generalized Least
Squares)
The estimates are compared with time series cross section regression
estimated using generalized least squares based on the following measures:
1. Robustness % = | − | 100%

2. Efficiency = () (if bias is not a serious problem
̂
2
̂
̂
= () + [()] (if bias is a serious problem)
3. Reliability (%) = 100

Where se = standard error of the bootstrap estimate and mean
= bootstrap estimate
∑ |− ̂|
4. Predictive Ability MAPE = X100 where NT is the total number of

observations.

3. Result
The mean among the estimates from twenty (20) data sets are used in the
evaluation. Note that the biases of β estimates from the proposed method
are generally tolerable while the biases of the generalized least squares
parameter estimates are generally not tolerable. The tolerable bias of the
parameter estimates from the proposed method can mean that the additivity
assumption of the backfitting algorithm is satisfied, and that the robustness
from the forward search algorithm is inherited by the proposed method.
In general, the behavior of the parameter estimates using the proposed
method is comparable to the generalized least squares estimates when there
is no perturbation in the data and when structural change is present in the
data (Table 2). Likewise, the behavior of the parameter estimates using the
proposed method is comparable to the generalized least squares estimates
in the presence of panel heterogeneity and a mixture of panel heterogeneity
and structural change.
Without perturbation or with structural change in the data, the proposed
method and the time series cross section regression (estimated using
generalized least squares) yields comparable β estimates which are both near
to the true value. In the presence of panel heterogeneity and a combination

12 | I S I W S C 2 0 1 9