Page 161 - Special Topic Session (STS) - Volume 2

STS474 Yoshihiro Y.

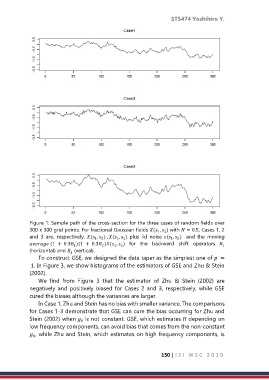
Figure 1: Sample path of the cross-section for the three cases of random fields over
300 x 300 grid points. For fractional Gaussian fields ( , ) with = 0.5, Cases 1, 2
1
2
and 3 are, respectively, ( , ) , ( , ) plus iid noise ( , ) and the moving
2
1
2
1
2
1
(1 + 0.3 )(1 + 0.3 )( , ) for the backward shift operators
2
1
1
2
1
(horizontal) and (vertical).
2
To construct GSE, we designed the data taper as the simplest one of =
1. In Figure 3, we show histograms of the estimators of GSE and Zhu & Stein
(2002).
We find from Figure 3 that the estimator of Zhu & Stein (2002) are
negatively and positively biased for Cases 2 and 3, respectively, while GSE
cured the biases although the variances are larger.
In Case 1, Zhu and Stein has no bias with smaller variance. The comparisons
for Cases 1-3 demonstrate that GSE can cure the bias occurring for Zhu and
Stein (2002) when is not constant. GSE, which estimates depending on
0
low frequency components, can avoid bias that comes from the non-constant
, while Zhu and Stein, which estimates on high frequency components, is
0
150 | I S I W S C 2 0 1 9