Page 164 - Special Topic Session (STS) - Volume 4

STS577 Md. Sabiruzzaman et al.

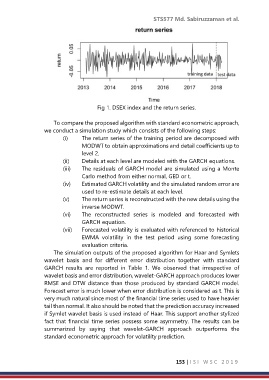
Fig 1. DSEX index and the return series.

To compare the proposed algorithm with standard econometric approach,
we conduct a simulation study which consists of the following steps:
(i) The return series of the training period are decomposed with
MODWT to obtain approximations and detail coefficients up to
level 2.
(ii) Details at each level are modeled with the GARCH equations.
(iii) The residuals of GARCH model are simulated using a Monte
Carlo method from either normal, GED or t.
(iv) Estimated GARCH volatility and the simulated random error are
used to re-estimate details at each level.
(v) The return series is reconstructed with the new details using the
inverse MODWT.
(vi) The reconstructed series is modeled and forecasted with
GARCH equation.
(vii) Forecasted volatility is evaluated with referenced to historical
EWMA volatility in the test period using some forecasting
evaluation criteria.
The simulation outputs of the proposed algorithm for Haar and Symlets
wavelet basis and for different error distribution together with standard
GARCH results are reported in Table 1. We observed that irrespective of
wavelet basis and error distribution, wavelet-GARCH approach produces lower
RMSE and DTW distance than those produced by standard GARCH model.
Forecast error is much lower when error distribution is considered as t. This is
very much natural since most of the financial time series used to have heavier
tail than normal. It also should be noted that the prediction accuracy increased
if Symlet wavelet basis is used instead of Haar. This support another stylized
fact that financial time series possess some asymmetry. The results can be
summarized by saying that wavelet-GARCH approach outperforms the
standard econometric approach for volatility prediction.

153 | I S I W S C 2 0 1 9