Page 232 - Contributed Paper Session (CPS) - Volume 3

CPS2002 Atina A. et al.
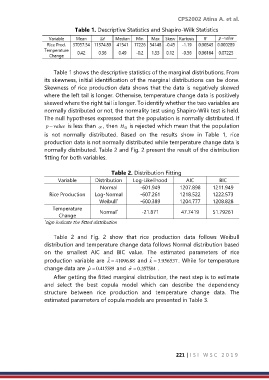
Table 1. Descriptive Statistics and Shapiro-Wilk Statistics

Table 1 shows the descriptive statistics of the marginal distributions. From
its skewness, initial identification of the marginal distributions can be done.
Skewness of rice production data shows that the data is negatively skewed
where the left tail is longer. Otherwise, temperature change data is positively
skewed where the right tail is longer. To identify whether the two variables are
normally distributed or not, the normality test using Shapiro-Wilk test is held.
The null hypotheses expressed that the population is normally distributed. If
p − value is less than  , then H is rejected which mean that the population
0
is not normally distributed. Based on the results show in Table 1, rice
production data is not normally distributed while temperature change data is
normally distributed. Table 2 and Fig. 2 present the result of the distribution
fitting for both variables.

Table 2. Distribution Fitting
Variable Distribution Log-Likelihood AIC BIC
Normal -601.949 1207.898 1211.949
Rice Production Log-Normal -607.261 1218.522 1222.573
*
Weibull -600.389 1204.777 1208.828
Temperature Normal -21.871 47.7419 51.79261
*
Change
* sign indicate the fitted distribution

Table 2 and Fig. 2 show that rice production data follows Weibull
distribution and temperature change data follows Normal distribution based
on the smallest AIC and BIC value. The estimated parameters of rice
ˆ
ˆ

production variable are = 41096 . 88 and = . 3 956537. While for temperature
k


change data are ˆ = . 0 415589 and ˆ = . 0 357584 .
After getting the fitted marginal distribution, the next step is to estimate
and select the best copula model which can describe the dependency
structure between rice production and temperature change data. The
estimated parameters of copula models are presented in Table 3.

221 | I S I W S C 2 0 1 9