Page 233 - Contributed Paper Session (CPS) - Volume 3

CPS2002 Atina A. et al.

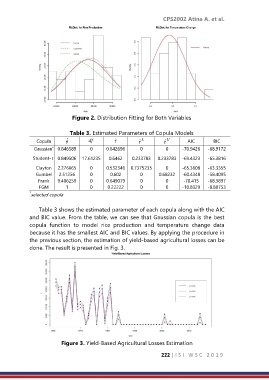
Figure 2. Distribution Fitting for Both Variables

Table 3. Estimated Parameters of Copula Models
ˆ
L
Copula  df  ˆ  ˆ  ˆ U AIC BIC
Gaussian 0.846589 0 0.642696 0 0 -70.9426 -68.9172
*
Student- t 0.849506 17.61235 0.6462 0.233783 0.233783 -69.4323 -65.3816
Clayton 2.276665 0 0.532346 0.7375235 0 -65.3608 -63.3355
Gumbel 2.51256 0 0.602 0 0.68232 -60.4348 -58.4095
Frank 9.406259 0 0.649079 0 0 -70.415 -68.3897
FGM 1 0 0.22222 0 0 -10.8329 -8.80753
* selected copula

Table 3 shows the estimated parameter of each copula along with the AIC
and BIC value. From the table, we can see that Gaussian copula is the best
copula function to model rice production and temperature change data
because it has the smallest AIC and BIC values. By applying the procedure in
the previous section, the estimation of yield-based agricultural losses can be
done. The result is presented in Fig. 3.

Figure 3. Yield-Based Agricultural Losses Estimation

222 | I S I W S C 2 0 1 9