Page 214 - Contributed Paper Session (CPS) - Volume 8

CPS2254 Dan C.
feature of Fathom, we were able to slow things down in generating a batch of
thirty trials, each time recording how many empty squares were in a trial.

It was important to run the initial “batch of 30 trials” on Fathom as slowly
as possible, so that students could see that everything Fathom was doing
mirrored the same ideas they had explored with their own paper recording
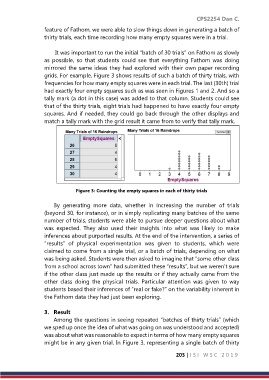
grids. For example, Figure 3 shows results of such a batch of thirty trials, with
frequencies for how many empty squares were in each trial. The last (30th) trial
had exactly four empty squares such as was seen in Figures 1 and 2. And so a
tally mark (a dot in this case) was added to that column. Students could see
that of the thirty trials, eight trials had happened to have exactly four empty
squares. And if needed, they could go back through the other displays and
match a tally mark with the grid result it came from to verify that tally mark.
Many Trials of 16 Raindrops

Many Trials of 16 Raindrops

Figure 3: Counting the empty squares in each of thirty trials

By generating more data, whether in increasing the number of trials
(beyond 30, for instance), or in simply replicating many batches of the same
number of trials, students were able to pursue deeper questions about what
was expected. They also used their insights into what was likely to make
inferences about purported results. At the end of the intervention, a series of
“results” of physical experimentation was given to students, which were
claimed to come from a single trial, or a batch of trials, depending on what
was being asked. Students were then asked to imagine that “some other class
from a school across town” had submitted these “results”, but we weren’t sure
if the other class just made up the results or if they actually came from the
other class doing the physical trials. Particular attention was given to way
students based their inferences of “real or fake?” on the variability inherent in
the Fathom data they had just been exploring.

3. Result
Among the questions in seeing repeated “batches of thirty trials” (which
we sped up once the idea of what was going on was understood and accepted)
was about what was reasonable to expect in terms of how many empty squares
might be in any given trial. In Figure 3, representing a single batch of thirty

203 | I S I W S C 2 0 1 9