Page 217 - Contributed Paper Session (CPS) - Volume 8

CPS2254 Dan C.
likelihood any given trial will have 6 raindrops or more on a square?” To gain
insight into that question, we ran 100 experiments on Fathom, where an
experiment was defined as “Count how many trials are needed to be run until
a trial hits 6 raindrops or more on any given square”.
Before running 100 experiments, we discussed what the results might look
like. Students knew an experiment could end with “one trial” because we could
get 6 or more drops on a square with the first trial. Some students thought an
experiment could go on for “thousands of trials” since maybe it would take a
while to get the desired result. We also noted that none of our initial
experimental data had that result. After discussion of initial expectations, we
ran Fathom for 100 experiments as defined above, and the results are in Figure
5.

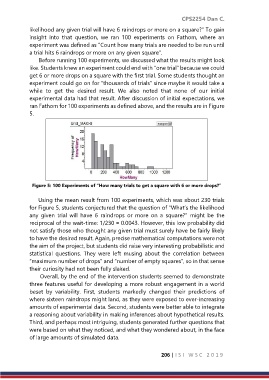
Figure 5: 100 Experiments of “How many trials to get a square with 6 or more drops?”

Using the mean result from 100 experiments, which was about 230 trials
for Figure 5, students conjectured that the question of “What’s the likelihood
any given trial will have 6 raindrops or more on a square?” might be the
reciprocal of the wait-time: 1/230 ≈ 0.0043. However, this low probability did
not satisfy those who thought any given trial must surely have be fairly likely
to have the desired result. Again, precise mathematical computations were not
the aim of the project, but students did raise very interesting probabilistic and
statistical questions. They were left musing about the correlation between
“maximum number of drops” and “number of empty squares”, so in that sense
their curiosity had not been fully slaked.
Overall, by the end of the intervention students seemed to demonstrate
three features useful for developing a more robust engagement in a world
beset by variability. First, students markedly changed their predictions of
where sixteen raindrops might land, as they were exposed to ever-increasing
amounts of experimental data. Second, students were better able to integrate
a reasoning about variability in making inferences about hypothetical results.
Third, and perhaps most intriguing, students generated further questions that
were based on what they noticed, and what they wondered about, in the face
of large amounts of simulated data.

206 | I S I W S C 2 0 1 9