Page 213 - Contributed Paper Session (CPS) - Volume 8

CPS2254 Dan C.
on paper a batch of at least thirty trials, we know could use Fathom to see a
batch of thirty trials within seconds.

Figure 1: A single trial (via Fathom)
The point in generating more data was to investigate some of the
question’s students had raised earlier, and here is where Fathom played a key
role. For example, Fathom could easily record how many “raindrops” were in
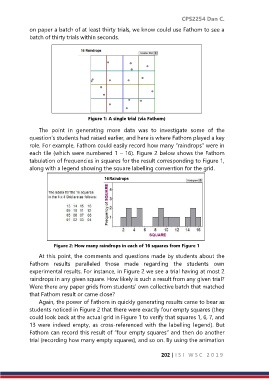
each tile (which were numbered 1 – 16). Figure 2 below shows the Fathom
tabulation of frequencies in squares for the result corresponding to Figure 1,
along with a legend showing the square labelling convention for the grid.

16 Raindrops

Figure 2: How many raindrops in each of 16 squares from Figure 1

At this point, the comments and questions made by students about the
Fathom results paralleled those made regarding the students own
experimental results. For instance, in Figure 2 we see a trial having at most 2
raindrops in any given square. How likely is such a result from any given trial?
Were there any paper grids from students’ own collective batch that matched
that Fathom result or came close?
Again, the power of Fathom in quickly generating results came to bear as
students noticed in Figure 2 that there were exactly four empty squares (they
could look back at the actual grid in Figure 1 to verify that squares 1, 6, 7, and
13 were indeed empty, as cross-referenced with the labelling legend). But
Fathom can record this result of “four empty squares” and then do another
trial (recording how many empty squares), and so on. By using the animation

202 | I S I W S C 2 0 1 9