Page 215 - Contributed Paper Session (CPS) - Volume 8

CPS2254 Dan C.
trials, we see a minimum of three and a maximum of eight empty squares. So,
what would be typical for the number of empty squares? If zero empty squares
was considered very unlikely (corresponding to one raindrop per square), then
wouldn’t one or two empty squares be fairly likely?

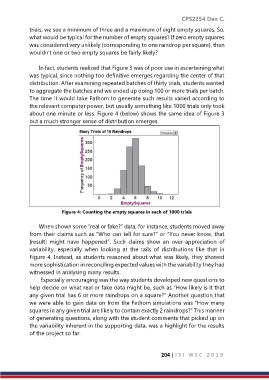
In fact, students realized that Figure 3 was of poor use in ascertaining what
was typical, since nothing too definitive emerges regarding the center of that
distribution. After examining repeated batches of thirty trials, students wanted
to aggregate the batches and we ended up doing 100 or more trials per batch.
The time it would take Fathom to generate such results varied according to
the relevant computer power, but usually something like 1000 trials only took
about one minute or less. Figure 4 (below) shows the same idea of Figure 3
but a much stronger sense of distribution emerges.

Many Trials of 16 Raindrops

Figure 4: Counting the empty squares in each of 1000 trials

When shown some “real or fake?” data, for instance, students moved away
from their claims such as “Who can tell for sure?” or “You never know, that
[result] might have happened”. Such claims show an over-appreciation of
variability, especially when looking at the tails of distributions like that in
Figure 4. Instead, as students reasoned about what was likely, they showed
more sophistication in reconciling expected values with the variability they had
witnessed in analysing many results.
Especially encouraging was the way students developed new questions to
help decide on what real or fake data might be, such as “How likely is it that
any given trial has 6 or more raindrops on a square?” Another question that
we were able to gain data on from the Fathom simulations was “How many
squares in any given trial are likely to contain exactly 2 raindrops?” This manner
of generating questions, along with the student comments that picked up on
the variability inherent in the supporting data, was a highlight for the results
of the project so far.

204 | I S I W S C 2 0 1 9