Page 100 - Contributed Paper Session (CPS) - Volume 1

CPS1158 Varun A. et al.
posterior samples. We carried out 1000 iterations and burn-in 200 to get the
approximate estimated values and recorded that generate sample is
convergent and stationary using Gelman-Rubin and Geweke test. Then, the
corresponding outcomes of posterior estimators and its standard deviation
are recorded in Table 1-2. From Table 1-2, one can easily conclude that
standard deviation is not much wider and its truly indicating the estimated
parameter values. We also obtained the credible interval in table 3 for
establishing the confidence interval of the estimated value and observed that
some parameters have not much significant affect on the series because its
intervals contain zero value.

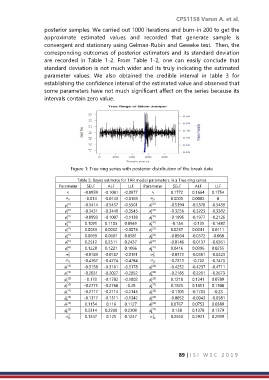
Figure 1: Tree ring series with posterior distribution of the break date

Table 5: Bayes estimate for TAR model parameters in a Tree ring series
Parameter SELF ALF LLF Parameter SELF ALF LLF
1 r -0.0959 -0.1081 -0.0977 2 r 0.1772 0.1664 0.1754
 11 -0.014 -0.0143 -0.0169  21 0.0005 0.0002 0
 1 ( 11 ) -0.5414 -0.5437 -0.5501 1  ( 21 ) -0.5394 -0.5378 -0.5489
2  ( 11 ) -0.3431 -0.3449 -0.3545 2  ( 21 ) -0.3256 -0.3223 -0.3382
3  ( 11 ) -0.0993 -0.1007 -0.1138  ( 3 21 ) -0.1995 -0.1977 -0.2126
4  ( 11 ) 0.1091 0.1105 0.0949 ( 4  21 ) -0.134 -0.135 -0.1482
5  ( 11 ) 0.0039 0.0032 -0.0074 5  ( 21 ) 0.0237 0.0241 0.0111
6  ( 11 ) 0.0669 0.0687 0.0581  ( 6 21 ) -0.0564 -0.0572 -0.068
7  ( 11 ) 0.2512 0.2511 0.2437 ( 7  21 ) -0.0146 -0.0137 -0.0261
8  ( 11 ) 0.1228 0.1221 0.1096  8 ( 21 ) 0.0416 0.0396 0.0255
2
 11 -0.0189 -0.0187 -0.0191  21 -0.0373 -0.0361 -0.0423
2
 12 -0.4767 -0.4774 -0.4784  22 -0.7211 -0.722 -0.7473
1  ( 12 ) -0.3158 -0.3161 -0.3178  1 ( 22 ) -0.4252 -0.4237 -0.4711
2  ( 12 ) -0.2031 -0.2027 -0.2052  2 ( 22 ) -0.2185 -0.2201 -0.2673
 ( 12 ) -0.178 -0.1782 -0.1802  ( 22 ) 0.1218 0.1241 0.0789
3 3
4  ( 12 ) -0.2775 -0.2768 -0.28  4 ( 22 ) 0.1825 0.1851 0.1308
5  ( 12 ) -0.2117 -0.2114 -0.2145  5 ( 22 ) -0.1701 -0.1703 -0.23
 6 ( 12 ) -0.1317 -0.1311 -0.1342  6 ( 22 ) -0.0052 -0.0043 -0.0581
7  ( 12 ) 0.1154 0.116 0.1127 7  ( 22 ) 0.0767 0.0753 0.0389
 8 ( 12 ) 0.2314 0.2298 0.2309  8 ( 22 ) 0.138 0.1378 0.1379
2
2
 12 0.1247 0.125 0.1247  22 0.2953 0.2921 0.2939

89 | I S I W S C 2 0 1 9