Page 101 - Contributed Paper Session (CPS) - Volume 1

CPS1158 Varun A. et al.

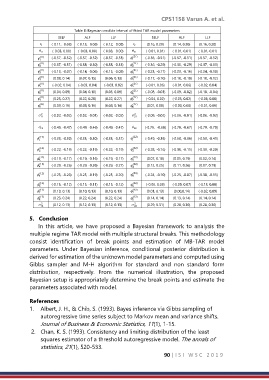
Table 8: Bayesian credible interval of fitted TAR model parameters
SELF ALF LLF SELF ALF LLF
1 r (-0.11, -0.08) (-0.13, -0.08) (-0.12, -0.08) 2 r (0.16, 0.20) (0.14, 0.20) (0.16, 0.20)
 (-0.03, 0.00) (-0.03, 0.00) (-0.03, -0.00)  21 (-0.01, 0.01) (-0.01, 0.01) (-0.01, 0.01)
11
 1 ( 11 ) (-0.57, -0.52) (-0.57, -0.52) (-0.57, -0.53) 1  ( 21 ) (-0.56, -0.51) (-0.57, -0.51) (-0.57, -0.52)
2  ( 11 ) (-0.37, -0.31) (-0.38, -0.30) (-0.38, -0.33) 2  ( 21 ) (-0.36, -0.29) (-0.36, -0.29) (-0.37, -0.31)
3  ( 11 ) (-0.13, -0.07) (-0.14, -0.06) (-0.15, -0.08)  3 ( 21 ) (-0.23, -0.17) (-0.23, -0.16) (-0.24, -0.18)
4  ( 11 ) (0.08, 0.14) (0.07, 0.15) (0.06, 0.13) 4  ( 21 ) (-0.17, -0.10) (-0.18, -0.10) (-0.18, -0.12)
5  ( 11 ) (-0.02, 0.04) (-0.03, 0.04) (-0.03, 0.02) 5  ( 21 ) (-0.01, 0.06) (-0.01, 0.06) (-0.02, 0.04)
6  ( 11 ) (0.04, 0.09) (0.04, 0.10) (0.03, 0.08)  6 ( 21 ) (-0.08, -0.03) (-0.09, -0.02) (-0.10, -0.04)
7  ( 11 ) (0.23, 0.27) (0.22, 0.28) (0.22, 0.27) 7  ( 21 ) (-0.04, 0.02) (-0.05, 0.02) (-0.06, 0.00)
8  ( 11 ) (0.09, 0.16) (0.08, 0.16) (0.08, 0.14)  8 ( 21 ) (0.01, 0.08) (-0.00, 0.08) (-0.01, 0.06)
2
 11 (-0.02, -0.02) (-0.02, -0.01) (-0.02, -0.02)  21 (-0.06, -0.02) (-0.06, -0.01) (-0.06, -0.02)
2
 12 (-0.49, -0.47) (-0.49, -0.46) (-0.49, -0.47)  22 (-0.76, -0.68) (-0.78, -0.67) (-0.79, -0.70)

1  ( 12 ) (-0.33, -0.30) (-0.33, -0.30) (-0.33, -0.31)  1 ( 22 ) (-0.49, -0.36) (-0.50, -0.36) (-0.53, -0.41)
2  ( 12 ) (-0.22, -0.19) (-0.22, -0.19) (-0.22, -0.19)  2 ( 22 ) (-0.28, -0.16) (-0.30, -0.15) (-0.33, -0.20)
 3 ( 12 ) (-0.19, -0.17) (-0.19, -0.16) (-0.19, -0.17)  3 ( 22 ) (0.07, 0.18) (0.05, 0.19) (0.02, 0.14)
4  ( 12 ) (-0.29, -0.26) (-0.29, -0.26) (-0.29, -0.27)  4 ( 22 ) (0.12, 0.25) (0.11, 0.26) (0.07, 0.19)
5  ( 12 ) (-0.23, -0.20) (-0.23, -0.19) (-0.23, -0.20)  5 ( 22 ) (-0.24, -0.10) (-0.25, -0.07) (-0.30, -0.15)

 6 ( 12 ) (-0.15, -0.12) (-0.15, -0.11) (-0.15, -0.12)  6 ( 22 ) (-0.06, 0.06) (-0.09, 0.07) (-0.13, 0.00)
7  ( 12 ) (0.10, 0.13) (0.10, 0.13) (0.10, 0.13) 7  ( 22 ) (0.03, 0.13) (0.00,0.14) (-0.02, 0.09)
 8 ( 12 ) (0.23, 0.24) (0.22, 0.24) (0.22, 0.24)  8 ( 22 ) (0.14, 0.14) (0.13, 0.14) (0.14, 0.14)
2
2
 12 (0.12, 0.13) (0.12, 0.13) (0.12, 0.13)  22 (0.29, 0.31) (0.28, 0.30) (0.28, 0.30)

5. Conclusion
In this article, we have proposed a Bayesian framework to analysis the
multiple regime TAR model with multiple structural breaks. This methodology
consist identification of break points and estimation of MB-TAR model
parameters. Under Bayesian inference, conditional posterior distribution is
derived for estimation of the unknown model parameters and computed using
Gibbs sampler and M-H algorithm for standard and non standard form
distribution, respectively. From the numerical illustration, the proposed
Bayesian setup is appropriately determine the break points and estimate the
parameters associated with model.

References
1. Albert, J. H., & Chib, S. (1993). Bayes inference via Gibbs sampling of
autoregressive time series subject to Markov mean and variance shifts.
Journal of Business & Economic Statistics, 11(1), 1-15.
2. Chan, K. S. (1993). Consistency and limiting distribution of the least
squares estimator of a threshold autoregressive model. The annals of
statistics, 21(1), 520-533.
90 | I S I W S C 2 0 1 9