Page 50 - Contributed Paper Session (CPS) - Volume 2

CPS1416 Jungtaek O. et al.
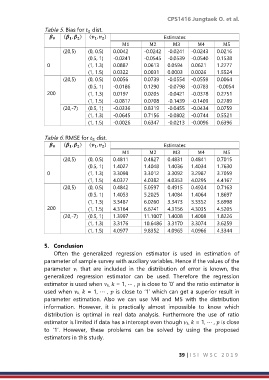
Table 5. Bias for dist.
5
( , ) ( , ) Estimates

M1 M2 M3 M4 M5
(20,5) (0, 0.5) 0.0042 -0.0242 -0.0241 -0.0243 0.0216
(0.5, 1) -0.0241 -0.0545 -0.0539 -0.0540 0.1538
0 (1, 1.3) 0.0887 0.0613 0.0594 0.0621 1.2777
(1, 1.5) 0.0322 0.0031 0.0003 0.0026 1.5524
(20,5) (0, 0.5) 0.0056 0.0739 -0.0554 -0.0559 0.0064
(0.5, 1) -0.0186 0.1290 -0.0798 -0.0783 -0.0054
200 (1, 1.3) 0.0197 0.0205 -0.0421 -0.0378 0.2751
(1, 1.5) -0.0817 0.0708 -0.1439 -0.1409 0.2789
(20,-7) (0.5, 1) -0.0336 0.8319 -0.0455 -0.0434 0.0759
(1, 1.3) -0.0645 0.7156 -0.0802 -0.0744 0.5521
(1, 1.5) -0.0026 0.6347 -0.0213 -0.0096 0.6396

Table 6. RMSE for dist.
5
( , ) ( , ) Estimates

M1 M2 M3 M4 M5
(20,5) (0, 0.5) 0.4811 0.4827 0.4831 0.4841 0.7015
(0.5, 1) 1.4027 1.4048 1.4036 1.4034 1.7630
0 (1, 1.3) 3.3098 3.3012 3.3092 3.2987 3.7059
(1, 1.5) 4.0377 4.0382 4.0353 4.0295 4.4167
(20,5) (0, 0.5) 0.4842 5.0597 0.4915 0.4924 0.7163
(0.5, 1) 1.4053 5.2025 1.4084 1.4064 1.8697
(1, 1.3) 3.3487 6.0260 3.3473 3.3352 3.6998
200 (1, 1.5) 4.3164 6.6741 4.3156 4.3035 4.5205
(20,-7) (0.5, 1) 1.3997 11.1007 1.4008 1.4008 1.8226
(1, 1.3) 3.3176 10.6486 3.3170 3.3074 3.6259
(1, 1.5) 4.0977 9.8352 4.0965 4.0966 4.3344

5. Conclusion
Often the generalized regression estimator is used in estimation of
parameter of sample survey with auxiliary variables. Hence if the values of the
parameter that are included in the distribution of error is known, the
generalized regression estimator can be used. Therefore the regression
estimator is used when , = 1, ⋯ , is close to ‘0’ and the ratio estimator is
used when , = 1, ⋯ , is close to ‘1’ which can get a superior result in
parameter estimation. Also we can use M4 and M5 with the distribution
information. However, it is practically almost impossible to know which
distribution is optimal in real data analysis. Furthermore the use of ratio
estimator is limited if data has a intercept even though , = 1, ⋯ , is close
to ‘1’. However, these problems can be solved by using the proposed
estimators in this study.

39 | I S I W S C 2 0 1 9