Page 17 - Contributed Paper Session (CPS) - Volume 3

CPS1923 Deemat C M. et al.
4.1. Monte carlo study. First we find the empirical type 1 error of the
proposed test. we simulate random sample from the exponential distribution
with cumulative distribution function () = 1 − exp(−), ≥ 0. Since the
test is scale invariant, we can take the scale parameter to be unity, while
performing the simulations. The empirical type 1 error for different values of
and is reported in Table 3. From the Table 3 it evident that the empirical type
1 error is a very good estimator of the size of the test even for small sample
size.
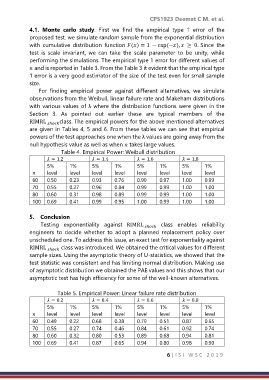
For finding empirical power against different alternatives, we simulate
obse,rvations from the Weibull, linear failure rate and Makeham distributions
with various values of λ where the distribution functions were given in the
Section 3. As pointed out earlier these are typical members of the
RIMRL ℎ class. The empirical powers for the above mentioned alternatives
are given in Tables 4, 5 and 6. From these tables we can see that empirical
powers of the test approaches one when the λ values are going away from the
null hypothesis value as well as when takes large values.
Table 4. Empirical Power: Weibull distribution
= 1.2 = 1.4 = 1.6 = 1.8
5% 1% 5% 1% 5% 1% 5% 1%
level level level level level level level level
60 0.50 0.23 0.93 0.76 0.99 0.97 1.00 0.99
70 0.55 0.27 0.96 0.84 0.99 0.99 1.00 1.00
80 0.60 0.31 0.98 0.89 0.99 0.99 1.00 1.00
100 0.69 0.41 0.99 0.95 1.00 0.99 1.00 1.00

5. Conclusion
Testing exponentiality against RIMRL ℎ class enables reliability
engineers to decide whether to adopt a planned replacement policy over
unscheduled one. To address this issue, an exact test for exponentiality against

RIMRL ℎ class was introduced. We obtained the critical values for different
sample sizes. Using the asymptotic theory of U-statistics, we showed that the
test statistic was consistent and has limiting normal distribution. Making use
of asymptotic distribution we obtained the PAE values and this shows that our
asymptotic test has high efficiency for some of the well-known alternatives.

Table 5. Empirical Power: Linear failure rate distribution
= 0.2 = 0.4 = 0.6 = 0.8
5% 1% 5% 1% 5% 1% 5% 1%
level level level level level level level level
60 0.49 0.22 0.68 0.38 0.79 0.51 0.87 0.65
70 0.55 0.27 0.74 0.46 0.84 0.61 0.92 0.74
80 0.60 0.32 0.80 0.53 0.89 0.68 0.94 0.81
100 0.69 0.41 0.87 0.65 0.94 0.80 0.98 0.90

6 | I S I W S C 2 0 1 9