Page 145 - Contributed Paper Session (CPS) - Volume 7

CPS2048 Md Zobaer H. et al.
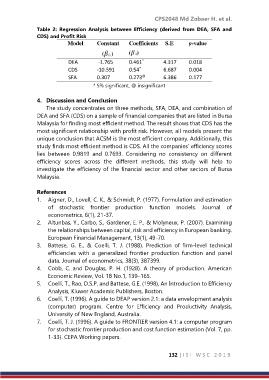
Table 2: Regression Analysis between Efficiency (derived from DEA, SFA and
CDS) and Profit Risk
Model Constant Coefficients S.E p-value
( 0 ) (1)
DEA -1.765 0.461 * 4.317 0.018
CDS -10.591 0.54 * 6.687 0.004
SFA 0.307 0.273 @ 6.386 0.177
* 5% significant, @ insignificant

4. Discussion and Conclusion
The study concentrates on three methods, SFA, DEA, and combination of
DEA and SFA (CDS) on a sample of financial companies that are listed in Bursa
Malaysia for finding most efficient method. The result shows that CDS has the
most significant relationship with profit risk. However, all models present the
unique conclusion that ACSM is the most efficient company. Additionally, this
study finds most efficient method is CDS. All the companies’ efficiency scores
lies between 0.9819 and 0.7693. Considering no consistency on different
efficiency scores across the different methods, this study will help to
investigate the efficiency of the financial sector and other sectors of Bursa
Malaysia.

References
1. Aigner, D., Lovell, C. K., & Schmidt, P. (1977). Formulation and estimation
of stochastic frontier production function models. Journal of
econometrics, 6(1), 21-37.
2. Altunbas, Y., Carbo, S., Gardener, E. P., & Molyneux, P. (2007). Examining
the relationships between capital, risk and efficiency in European banking.
European Financial Management, 13(1), 49-70.
3. Battese, G. E., & Coelli, T. J. (1988). Prediction of firm-level technical
efficiencies with a generalized frontier production function and panel
data. Journal of econometrics, 38(3), 387399.
4. Cobb, C. and Douglas, P. H. (1928). A theory of production. American
Economic Review, Vol. 18 No.1, 139–165.
5. Coelli, T., Rao, D.S.P. and Battese, G.E. (1998), An Introduction to Efficiency
Analysis, Kluwer Academic Publishers, Boston.
6. Coelli, T. (1996). A guide to DEAP version 2.1: a data envelopment analysis
(computer) program. Centre for Efficiency and Productivity Analysis,
University of New England, Australia.
7. Coelli, T. J. (1996). A guide to FRONTIER version 4.1: a computer program
for stochastic frontier production and cost function estimation (Vol. 7, pp.
1-33). CEPA Working papers.

132 | I S I W S C 2 0 1 9