Page 85 - Contributed Paper Session (CPS) - Volume 1

CPS1110 Selamawit M. et al.
with = 0.2 and () being the indicator function taking value 1 if A is true
0
and value 0 else. The associated band width ℎ remain to be defined.

Case B: Gaussian kernel model
The likelihood estimates are denoted (|): ∈ Ω , and they are
̂

based on a Gaussian kernel function,

with the (2 × 2)-matrix Σ being the empirical covariance matrix of the the
̂

corresponding set of observations . The associated band width ℎ remain

to be defined. For the traditional Markov chain model with stationary class
proportions along the profile, we use,

As prior trend Markov chain model we use the marginals ; ∈ , and the
0

transition matrix above as reference matrix . The trend prior model () is

computed by the approach defined in Moja et al. (2018).

0.9

QN 0.7

0.5

0.3
0.25 0.50 0.75 1.0
FN
(a) (b)

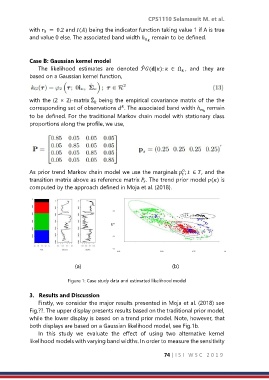
Figure 1: Case study data and estimated likelihood model

3. Results and Discussion
Firstly, we consider the major results presented in Moja et al. (2018) see
Fig.??. The upper display presents results based on the traditional prior model,
while the lower display is based on a trend prior model. Note, however, that
both displays are based on a Gaussian likelihood model, see Fig.1b.
In this study we evaluate the effect of using two alternative kernel
likelihood models with varying band widths. In order to measure the sensitivity

74 | I S I W S C 2 0 1 9