Page 106 - Contributed Paper Session (CPS) - Volume 2

CPS1443 Shogo H.N. et al.
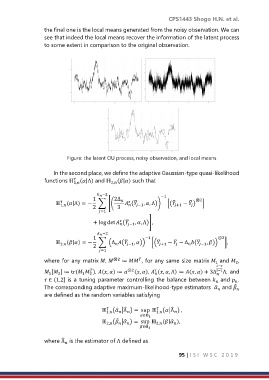
the final one is the local means generated from the noisy observation. We can
see that indeed the local means recover the information of the latent process
to some extent in comparison to the original observation.

Figure: the latent OU process, noisy observation, and local means

In the second place, we define the adaptive Gaussian-type quasi-likelihood

functions ℍ 1, (|Λ) and ℍ 2, (|) such that

−2
1 2Δ −1 ⊗2
̅
̅

̅
ℍ (|Λ) = − ∑ [( ( −1 , , Λ)) [( +1 − ) ]
1,

2 3
=1

̅
+ log det ( −1 , , Λ)] ,

−2
1 −1 ⊗2
̅
̅
̅
̅
ℍ 2, (|) = − ∑ (Δ ( −1 , )) [( +1 − − Δ ( −1 , )) ],

2
=1

where for any matrix , ⊗2 ≔ , for any same size matrix and ,
2
1
2−

[ ] ≔ tr( ), (, ) ≔ ⊗2 (, ), (, , Λ) ≔ (, ) + 3Δ −1 Λ, and
2
1

1
2

∈ (1,2] is a tuning parameter controlling the balance between and .

The corresponding adaptive maximum-likelihood-type estimators ̂ and
̂

are defined as the random variables satisfying

̂
̂
ℍ 1, (̂ |Λ ) = sup ℍ 1, (|Λ ) ,

∈Θ 1
̂
ℍ 2, ( |̂ ) = sup ℍ 2, (|̂ ),

∈Θ 2

where Λ is the estimator of Λ defined as
̂

95 | I S I W S C 2 0 1 9