Page 231 - Contributed Paper Session (CPS) - Volume 2

CPS1844 Reza M.
2
2
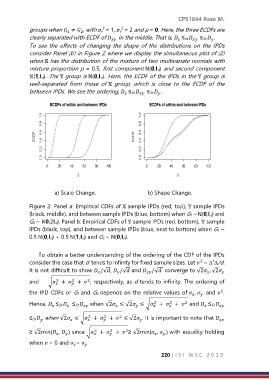
groups when ≠ , with σx = 1, σy = 2 and µ = 0. Here, the three ECDFs are
1
2
clearly separated with ECDF of in the middle. That is, ≤St ≤St .

To see the effects of changing the shape of the distributions on the IPDs
consider Panel (b) in Figure 2 where we display the simultaneous plot of (2)
when has the distribution of the mixture of two multivariate normals with
mixture proportion p = 0.5, first component ℕ(0,Id) and second component
ℕ(1,Id). The group is ℕ(0,Id). Here, the ECDF of the IPDs in the group is
well-separated from those of group, which is close to the ECDF of the
between IPDs. We see the ordering, ≤St ≤St .

a) Scale Change. b) Shape Change.

Figure 2: Panel a: Empirical CDFs of sample IPDs (red, top), sample IPDs
(black, middle), and between sample IPDs (blue, bottom) when G1 ∼N(0,Id) and
G2 ∼ ℕ0,2Id). Panel b: Empirical CDFs of sample IPDs (red, bottom), sample
IPDs (black, top), and between sample IPDs (blue, next to bottom) when G1 ∼
0.5 ℕ(0,Id) + 0.5 ℕ(1,Id) and G2 ∼ ℕ(0,Id).

To obtain a better understanding of the ordering of the CDF of the IPDs
consider the case that d tends to infinity for fixed sample sizes. Let = ∆’∆/d.
2
It is not difficult to show /√, /√ and /√ converge to √2 , √2

and √ + + , respectively, as d tends to infinity. The ordering of
2
2
2

the IPD CDFs or G1 and G2 depends on the relative values of , and .
2

2
2
2
Hence, ≤St ≤St when √2 ≤ √2 ≤ √ + + and ≤St

2
2
2
≤St when √2 ≤ √ + + ≤ √2 . It is important to note that

≥ √2min( , ) since √ + + ≥ √2min( , ) with equality holding
2
2
2

when = 0 and =

220 | I S I W S C 2 0 1 9