Page 100 - Contributed Paper Session (CPS) - Volume 2

CPS1442 Uzuke C.A. et al.
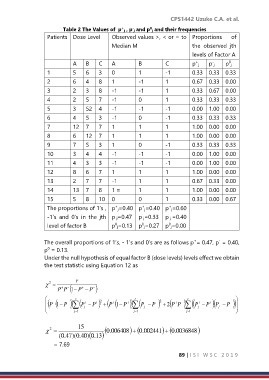
Table 2 The Values of p j , p j and p j and their frequencies
+
-
0
Patients Dose Level Observed values >, < or = to Proportions of
Median M the observed jth
levels of Factor A
A B C A B C p j p j p j
0
-
+
1 5 6 3 0 1 -1 0.33 0.33 0.33
2 6 4 8 1 -1 1 0.67 0.33 0.00
3 2 3 8 -1 -1 1 0.33 0.67 0.00
4 2 5 7 -1 0 1 0.33 0.33 0.33
5 3 52 4 -1 -1 -1 0.00 1.00 0.00
6 4 5 3 -1 0 -1 0.33 0.33 0.33
7 12 7 7 1 1 1 1.00 0.00 0.00

8 6 12 7 1 1 1 1.00 0.00 0.00
9 7 5 3 1 0 -1 0.33 0.33 0.33
10 3 4 4 -1 -1 -1 0.00 1.00 0.00
11 4 3 3 -1 -1 -1 0.00 1.00 0.00
12 8 6 7 1 1 1 1.00 0.00 0.00
13 2 7 7 -1 1 1 0.67 0.33 0.00
14 13 7 8 1 = 1 1 1.00 0.00 0.00

15 5 8 10 0 0 1 0.33 0.00 0.67
+
+
The proportions of 1’s , p j=0.40 p j=0.40 p j=0.60
+
-
-
-
-1’s and 0’s in the jth p j=0.47 p j=0.33 p j =0.40
0
0
0
level of factor B p j=0.13 p j=0.27 p j=0.00

-
+
The overall proportions of 1’s, - 1’s and 0’s are as follows p = 0.47, p = 0.40,
p = 0.13.
0
Under the null hypothesis of equal factor B (dose levels) levels effect we obtain
the test statistic using Equation 12 as
r
 2 =
P + P − ( − P1 + − P − )
 − − c + + 2 + + c − − 2 + − c + + − − 



+
 ( (  P 1 − P )) (P j − P ) ( + P ( − P1 )) (P j − P ) ( PP2 ) (( P j − P )(P j − P )) 
 = j 1 = j 1 = j 1 

15
 2 = ( 006408.0 ) ( 002441.0+ ) ( 0036848.0+ )
. 0 ( 47 )( . 0 40 ) ( 13.0 )
= 7.69
89 | I S I W S C 2 0 1 9