Page 132 - Contributed Paper Session (CPS) - Volume 2

CPS1461 Michal P. et. al

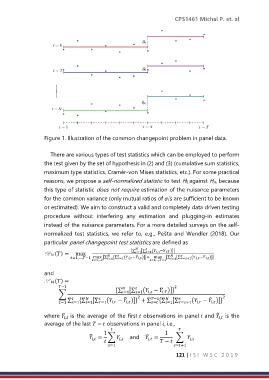
Figure 1. Illustration of the common changepoint problem in panel data.

There are various types of test statistics which can be employed to perform
the test given by the set of hypothesis in (2) and (3) (cumulative sum statistics,
maximum type statistics, Cramér-von Mises statistics, etc.). For some practical
reasons, we propose a self-normalized statistic to test H0 against HA, because
this type of statistic does not require estimation of the nuisance parameters
for the common variance (only mutual ratios of σi’s are sufficient to be known

or estimated). We aim to construct a valid and completely data driven testing
procedure without interfering any estimation and plugging-in estimates
instead of the nuisance parameters. For a more detailed surveys on the self-
normalized test statistics, we refer to, e.g., Pes ̌ta and Wendler (2018). Our
particular panel changepoint test statistics are defined as

|∑ =1 [∑ =1 ( , − ̅ , )]|
R N () = max
=1,…,−1 max |∑ =1 [∑ =1 ( , − ̅ )]|+ max |∑ =1 [∑ =+1 ( , − ̃ )]|
,
,
=1,… =,…,−1

and
S N () =
−1 2
̅
{∑ =1 [∑ =1 ( − )]}
,
,
∑ 2 2
̅
̃
∑ {∑ [∑ ( − )]} + ∑ −1 {∑ [∑ ( − )]}
=1 =1 =1 =1 , , = =1 =+1 , ,

where is the average of the first observations in panel and is the
̃
̅
,
,
average of the last − observations in panel , i.e.,

1 1
̅
̃
= ∑ and = ∑
,
,
,
,
−
=1 =+1
121 | I S I W S C 2 0 1 9